
1. 금속의 결정체
금속은 고체상태(solid state)에서 결정을 이루고 있다. 보통 금속은 크고 작은 수많은 결정입자가 무질서한 상태로 집합되어 있는 다결정체이다. 그리고 결정입자와 결정입자의 경계를 결정경계(grain boundary)라 하고, 1개의 결정입자를 X선으로 보면, 원자들이 규칙적으로 배열되어 있다. 이와 같은 배열을 결정격자 또는 공간격자(space lattice)라 하고, 각각의 공간격자를 구성하는 단위부분을 단위포(unit cell)라 하며, 금속은 각각 고유의 결정격자를 가지고 있다.

<공간격자, 단위포>
(a)는 공간격자이고, (b)는 단위포이다. 공간격자는 기본적으로는 공간의 점의 배열이지만, 이해하기 쉽게 하기 위해 이것을 도시할 때에는 이 점을 선으로 연결한다.
단위포의 입체적인 3축 방향의 길이 a, b, c를 격자상수(lattice constant)라고 하며, 이 크기는 10-6㎝=1Å의 수 배 정도이고, 또 두 축 사이의 각을 각각 α, β, γ라 하며 축 사잇각(axial angle)이라고 한다.
2. 금속의 결정계와 결정격자
결정격자의 원자배열은 금속의 종류, 온도 및 대칭성 등에 따라 다르고, 그 성질에도 많은 영향을 미친다. 금속의 결정형(crystal model)에는 7종이 있으나 결정격자는 14종으로 세분된다.
순금속의 결정구조는 일부 비금속에 가까운 특수한 원소(In, Sn, Te, Tl, Bi)를 제외하면 대부분은 입방정계의 체심입방격자 및 면심입방격자와 조밀육방격자이다.

<결정계와 결정격자>

<주요 금속의 격자상수>
중요한 금속의 격자상수이며, 14종의 브라베(Bravais)격자를 나타낸 것이다.


<브라베의 격자>
3. 밀러 지수(Miller Index)
입방정의 단위격자의 만나는 한 점을 원점으로 하여 3차원의 좌표계를 생각하고 격자상수를 단위로 하여 길이를 나타내면 각 원자의 위치는 아래 그림에 나타낸 것과 같이 된다. 그러나 결정의 구조를 생각할 때에는 각각의 원자위치를 나타내는 것보다는 원자로 구성되는 면(plane)이나 원자배열의 방향을 상대적으로 나타내는 것이 좋다. 면이나 방향의 표시에는 결정학에서 쓰이는 밀러지수(Miller index)
를 이용하는데, 이 표시법에 있어서 결정면은 그 면에 의한 좌표축의 각 절편길이의 역수를 최소정수비로
나타내며, 또 결정방향은, 방향을 나타내는 직선이 원점을 지난다고 할 때 그 직선 위의 임의의 한 점의 좌
표의 최소정수비로 나타낸다. 그리고 이와 같이해서결정한 면의 지수를 h, k, ℓ 방향의 지수를 u, v, w라
고 하면 면은 (hkℓ) 방향은〔u v w〕라고 표시한다.
또 지수가 마이너스(-)인 경우에는 (hkℓ),〔 u v w〕등과 같이 숫자 위에 -부호를 붙인다
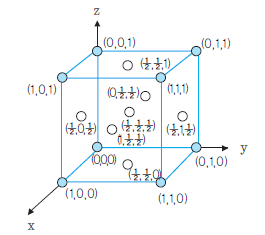
<원자 위치의 좌표>
가. 입방정계의 밀러지수
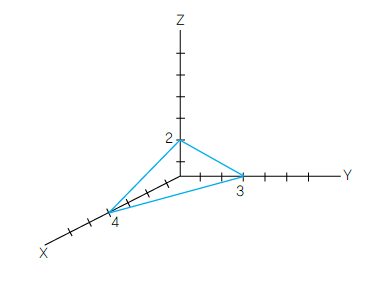
<면(346)의 밀러지수>
x, y, z축의 절편의 길이 ‥‥‥‥‥‥‥‥ 4, 3, 2
그 역수 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ , ,
최소정수비 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 3, 4, 6
따라서, 이 면의 밀러 지수는 (3 4 6)이 된다.
또 그림과 같은 3개의 평행면을 생각하면, 면 A 면 B 면 C
절편의 길이 1, 1, 1 2, 2, 2 3, 3, 3
역수 1, 1, 1 , , , ,
면의 밀러 지수 (1 1 1) (1 1 1) (1 1 1)
방향의 밀러지수 표시법을 설명하면, 그 방향으로 평행이고 원점을 지나는 직선을 생각하여 그 위에 적당한 점 A를 택한다. 이 점의 좌표는 1, 2, 1이며, 따라서 이 방향의 밀러지수는 [121]이라고 쓴다. 만일 직선 위의 한 점으로써 B점을 택하였다면 밀러 지수는 [242]가 될 것이지만 최소정수비로 고치면 [121]이 된다. 즉, 이 지수의 결정법으로 알 수 있듯이, 이 직선에 평행한 방향은 모두 같은 지수로 나타낼 수 있다. 면을 표시할 때에는 절편의 길이의 역수를 취하나 방향을 표시할 경우는 좌표의 값이 그대로 쓰인다는 것을 알아야 한다.
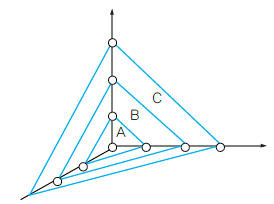
<평행한 면(111)의 밀러지수>
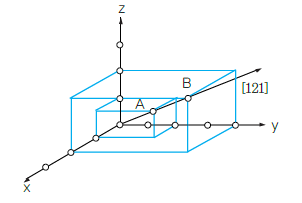
<121 방향의 밀러지수>
입방정계에 있어서 중요한 면과 방향의 밀러지수를 나타내고 있다.
이 그림의 [110] 방향과 (110)면의 관계로부터 알 수 있는 것과 같이 입방격자에서는 지수가 같은 면과 방향은 반드시 직교한다.
또한 (100), (010), (001) 및 (001), (100), (010)의 6개의 면은 좌표축에 대한 상대적인 대칭성은 똑같다. 이와 같은 면이나 방향을 등가(equivalent)한다고 하며, 등가한 면이나 방향을 일괄하여 표시하고자 할 때에는 그 중에 하나로, 등가한 면은 {h k l}, 등가한 방향은 <u, v, w>라고 쓴다.
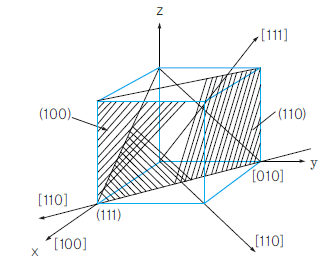
<입방정계의 중요 밀러 지수>
나. 육방정계의 밀러지수
육방정계에 관하여도 입방정계에서와 같이 면지수가 사용되며,그림과 같이 육방격자의 단위포는 동일면 위에 있어서 서로 120°로 교차하는 a축과 a축에 수직한 c축 즉 a1, a2, a3, c의 4개의 좌표축에 대응하는 4개의 지수가 필요하다.
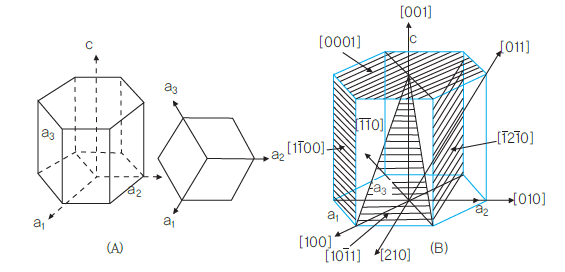
<육방정계의 좌표축(a)과 중요 밀러지수(b)>
따라서 육방정계 면의 밀러지수는 (hkiℓ)로 표시하며, 이 지수를 밀러-브라베 지수(Miller-Bravais indices)라고 한다. 그리고 h, k, i는 3개의 a축 a1, a2, a3축에 대하여, ℓ은 c축에 대하여, 각각 만나는 점까지의 길이와 단위길이에 대한 비의 역수이며, i는 h와 k에 의해서 결정되는 것으로서, h+k+i=0, h+k=i의 관계가 있고, 결정면은 h, k, ℓ의 3점으로 결정된다. 따라서 (hkℓ)과 같이 3개의 지수로 표시하는 방법도 있다.
육방정계의 대표적인 면으로는 {0001}인 기준 밑면(basal plane)과 {1010}의 각통면 (prismatic plane)과 {1011}의 각뿔면(pyramidal plane)이 있으며, 같은 지수를 갖는 면과 방향의 직교성은 수직축에 평행한 면 이외에 육방정계의 경우는 성립하지 않는다.
육방정계에서의 방향도 4개의 지수를 사용하여 [uvtw]와 같이 표시하며, 면지수에서와 같이 다음과 같은 관계가 있다.
u+v+t=0, u+v=t 의 관계가 있으므로 육방정계의 방향도 a1, α2, c의 3개축에 의해 [uvw]와 같이 표
시할 때도 많다. 이때의 변환 [uvtw]→[uvw]는
U=v-t
V=v-t
W=w
에 의하여 나타낼 수도 있다.
예를 들면,
[1010]=[210]
[1120]=[330]
=[110]
'ㆍ공부 자료 > ㆍ금속재료' 카테고리의 다른 글
| 13. 금속재료-금속가공 (2) | 2024.08.05 |
|---|---|
| 12. 금속재료-결정구조 (3) | 2024.08.02 |
| 10. 금속재료-금속조직 (3) | 2024.07.27 |
| 9. 금속재료-금속조직 (5) | 2024.07.22 |
| 8. 금속재료-금속조직 (0) | 2024.07.21 |



